Historias de Pi: calculando el área del círculo
En una entrada previa, reflexionamos sobre le relación entre la longitud de una circunferencia y su diámetro, que, como aprendimos en la escuela, es el número π . Una relación similar ocurre cuando queremos calcular el área de un círculo, que sabemos es el cuadrado del radio multiplicado por π. Pero esta relación de proporcionalidad , intuitiva sin duda, tampoco es tan evidente.
Estos teoremas de la geometría (pues eso son) que se enuncian tan fácilmente y que aprendemos de manera universal, tienen demostraciones muy sutiles. Ya vimos en la entrada aludida que la prueba del correspondiente a la longitud de una circunferencia descansa en una noción que los matemáticos tardaron siglos en formalizar adecuadamente, la de límite (o si se quiere, la de su prima hermana, la derivada).
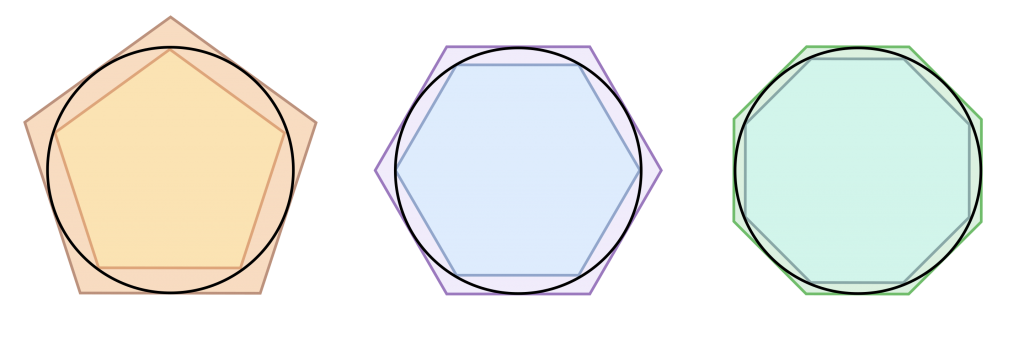
Una primera prueba de que el área de un círculo de radio r es A = π r2 se debe a Arquímedes. Si pensamos en una sucesión de polígonos regulares inscritos en el círculo, sabemos que el área de cada uno de ellos es la mitad del perímetro multiplicado por la distancia del centro a sus lados (la apotema). Si imaginamos ahora al límite (por ejemplo, cuando el número de lados tiende a infinito), entonces
A = ½ x 2 π r x r
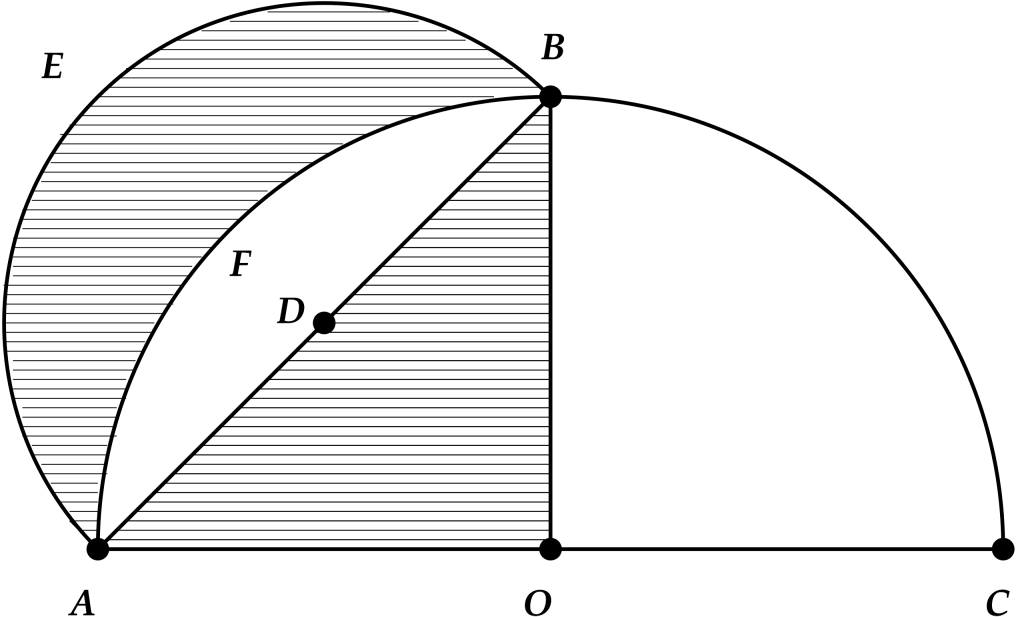
Previo a Arquímedes, Hipócrates de Quíos (470 a.C.-410 a. C.) probó que el área de un círculo era proporcional al cuadrado del diámetro, cuando trataba de resolver el problema de la cuadratura del círculo (construir un cuadrado con el mismo área de un círculo dado solamente con regla y compás). Hipócrates lo quiso resolver con el llamado problema de la cuadratura de la lúnula (veáse la figura 1).
Arquímedes utilizó el llamado método exhaustivo, introducido por Eudoxo de Cnido (390 a. C.-37 a. C) introdujo el método exhaustivo, un antecedente del cálculo integral, para probar que el área de un círculo era proporcional al cuadrado del radio. En el razonamiento de Arquímedes, en el paso al límite, se usa de una manera no rigurosa pero acertada como las secantes (los lados de los polígonos) se aproximan a la longitudes de arco, y las apotemas al radio.
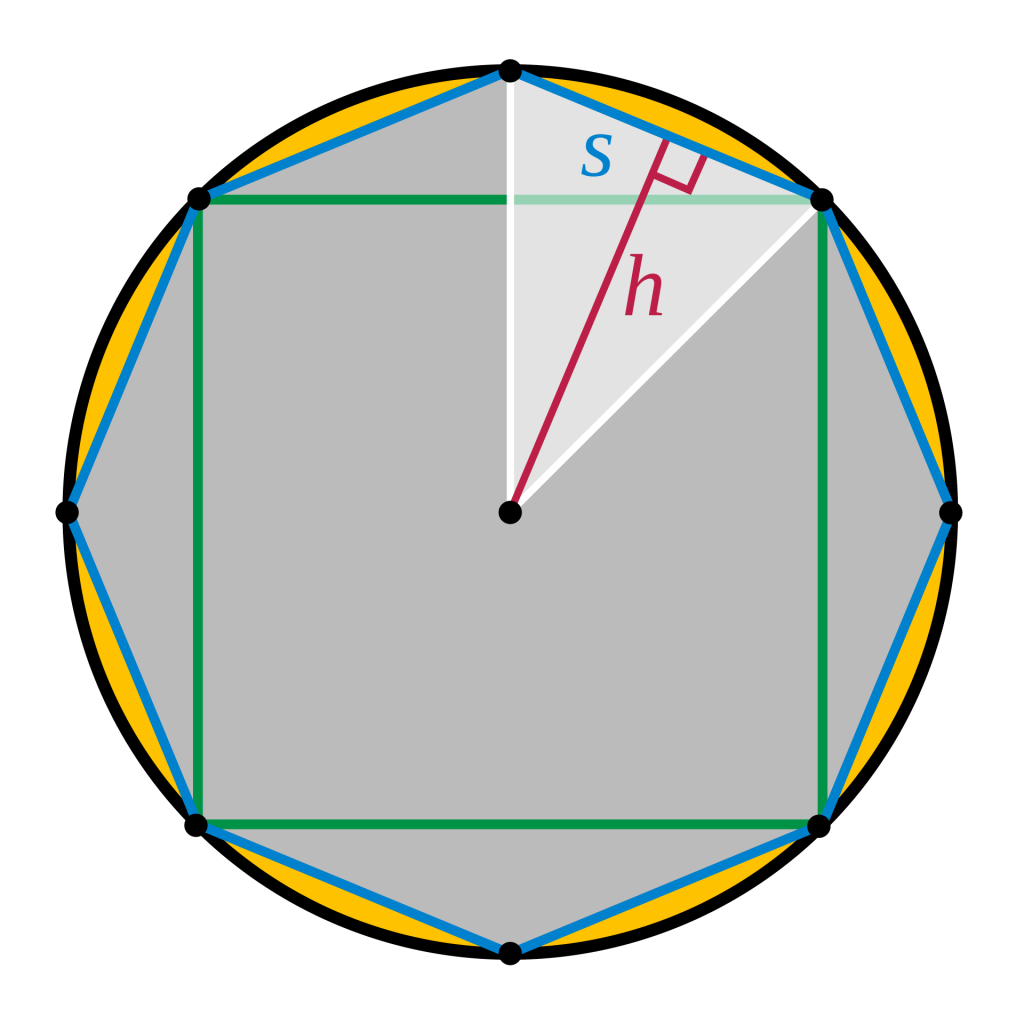
Es interesante recordar los argumentos de Arquímedes. Primero, compara el área del círculo con la de un triángulo rectángulo cuya base mida lo mismo que la longitud de la circunferencia y cuya altura sea el radio. Entonces razona: supongamos que no coincidan, o sea que será mayor o menor, y en cada caso, llega a una contradicción. ¿Qué tiene esto que ver con los polígonos inscritos? Sea A el área del círculo y a la del triángulo, y sea E el exceso en el caso de que A sea mayor que a = 1⁄2cr, donde c es la longitud de circunferencia y r el radio. Inscribimos un cuadrado en el círculo, y nos quedan cuatro segmentos iguales. Sea S4 el área de esos cuatro segmentos y supongamos que S4 es mayor que E. Si ese es el caso, divido cada segmento en dos y obtenemos un octógono. Hacemos lo mismo, contamos el área de esos ocho segementso, que será S8 . De nuevo, vemos si es mayor que E, y así hasta que lleguemos a un polígono de n lados tal que el correspondiente área Sn sea menor que E. Entonces el área del polígono será Pn = A – Gn, mayor que la del triángulo.
Y ahora llega la contradicción. Trazamos una apotema de longitud h. Si cada lado del polígono mide s, entonces el perímetro, ns, es menor que c. El área del polígono es ½ nsh. Como h es menor que r y ns menor que c, el área del polígono debe ser menor que la del triángulo, lo que es una contradicción.
El argumento en el otro caso funciona de manera parecida, y en consecuencia, debe darse la igualdad.
Hoy en día tenemos instrumentos mucho más precisos. La integración nos permite calcular el área de un círculo de varias formas, muy elegantes y sencillas.
Me gustaría terminar con una reflexión sobre el ingenio de los matemáticos de otras épocas, que sin contar con las técnicas del cálculo diferencial e integral fueron capaces de obtener logros que ahora nos parecen evidentes.
___________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).
Muy bueno
I don’t like math, but it was interesting to read. Thanks to the author, it is clear that he really tried when writing.
[…] área de un círculo es la cantidad de espacio que ocupa dentro de su límite. La fórmula para calcular el área (A) es […]
Nice info. Thanks for Sharing
Nice info. Thanks for Sharing
Thanks for such a thoughtful write-up!
Reflexionemos sobre la relación entre la longitud de una circunferencia y su diámetro, que, como aprendimos en la escuela, está determinada por el número π. Una relación similar aparece cuando queremos calcular el área de un círculo: sabemos que se obtiene multiplicando π por el cuadrado del radio. Sin embargo, aunque esta relación de proporcionalidad nos resulte intuitiva, no es tan evidente a simple vista.
Thanks for such a great write-up!
¡Qué buen seguimiento al post anterior sobre la circunferencia! Me encanta cómo conectas la longitud con el área del círculo, usando el omnipresente π. Es fascinante pensar en esa ‘relación de proporcionalidad’ que mencionas y cómo se aplica de manera tan fundamental en geometría. ¡Ya quiero leer más!
основанием для вызова специалиста является неспособность человека самостоятельно выйти из состояния непрерывного употребления алкоголя и наличие признаков абстиненции.
Разобраться лучше – вывод из запоя цена сочи
Вывод из запоя в клинике и на дому в Сочи: лечение алкоголизма, капельница, детоксикация, помощь нарколога круглосуточно, анонимно и безопасно.
Изучить вопрос глубже – вывод из запоя с выездом сочи
I enjoyed reading this article a lot. The explanations are straightforward, helpful, and pleasant to follow. TMTCash
Соблюдаем конфиденциальность, бережно общаемся с пациентом и его близкими на каждом этапе.
Исследовать вопрос подробнее – вызов нарколога на дом
Нарколог на дом в Казани — это срочная медицинская помощь пациенту при запое, похмелья, интоксикации, абстинентного синдрома, наркотической ломки и других ситуациях, когда человеку сложно самостоятельно обратиться в клинику. Врач приезжает на дом, проводит осмотр, диагностику состояния, подбирает препараты, ставит капельница и дает рекомендации по дальнейшему лечению зависимости.
Получить дополнительные сведения – вызвать нарколога на дом казань
Слушайте кто искал участок То вообще непонятно где смотреть Соседи какие Короче, работает быстро и бесплатно — публичная кадастровая карта россии онлайн Скачал выписку сразу В общем, вся инфа вот здесь — карта кадастровая публичная https://publichnaya-kadastrovaya-karta-abc.ru Пользуйтесь нормальной картой Перешлите тому кто ищет участок
Вывод из запоя на дому удобен, когда пациенту тяжело посещать клинику, когда близкого человека нельзя оставить одного или когда необходимо быстро получить помощь без поездки в больницы. Нарколог приезжает на место, проводит обследование, фиксирует жалобы, проверяет давление, пульс, насыщение кислородом, оценивает риски и затем назначает лечение запоя.
Получить дополнительную информацию – https://vyvod-is-zapoya-sochi24.ru/
Запоя вывод в клинике Сочи: лечение алкогольной зависимости, капельница, детоксикация, помощь нарколога на дому, кодирование и реабилитация анонимно
Узнать больше – вывод из запоя на дому цена сочи
В Москве помощь при запое может проводиться на дому, в клинике, в наркологическом центре или в стационаре. Домашний формат подходит, если пациент находится в сознании, контактирует с врачом и нет признаков тяжелого психоза, судорог, опасного поведения или выраженного нарушения дыхания. Если состояние тяжелое, нарколог может рекомендовать стационарное лечение, потому что в клинике доступно круглосуточно организованное наблюдение, диагностика, ЭКГ, анализ крови, коррекция терапии и контроль осложнений.
Получить дополнительные сведения – вывод из запоя в москве в стационаре
This was a great read. I appreciate the clear explanations and the effort put into creating such high-quality content. TMTCash88 Paldo
Вызов нарколога на дом в Казани. Круглосуточная наркологическая помощь на дому: лечение запоя, детоксикация, капельница, консультация. Анонимный прием. Узнайте цену в клинике.
Подробнее можно узнать тут – нарколог на дом цена в казани
Вывод из запоя в Сочи требуется, когда человек не может самостоятельно прекратить употребление алкоголя, испытывает похмелья, признаки ломки, тревогу, бессонницу, рвоту, сильную слабость или резкое ухудшение самочувствие. Даже если запой длится несколько дней, риск осложнений остается высокий: страдают системы организма, печень, сердце, сосуды, нервная система, психика и общее состояние здоровья.
Углубиться в тему – наркология вывод из запоя сочи
Вывод из запоя — это только первый шаг в лечении алкогольной зависимости. Без последующей терапии риск рецидива очень высок. Наш наркологический центр предлагает полный курс лечения алкоголизма, включая кодирование и психотерапию. Кодирование на дому проводится различными методами: уколом (Торпедо, Эспераль, Налтрексон, Аквилонг), медикаментозным вшиванием (дисульфирам, Вивитрол), гипнозом по Довженко, а также двойным блоком. Каждый метод подбирается врачом индивидуально, с согласия пациента и при отсутствии противопоказаний. Опытный нарколог объяснит, какая кодировка подойдёт именно вам, учитывая стаж и форму зависимости.
Получить больше информации – chastnyj-narkolog-na-dom-telefon
Вывод из запоя на дому подходит пациентам, которым необходимо получить помощь в привычной обстановке. Вызов врача можно заказать в любое время суток: выездная бригада приезжает по указанному адресу, проводит осмотр, оценивает давление, пульс, степень интоксикации, риск психозов, галлюцинаций, судорожных реакций, инфаркта, инсульта и других осложнений.
Исследовать вопрос подробнее – вывод из запоя капельница
Buen artículo sobre “Historias de Pi: calculando el área del círculo”; se nota el cuidado en la explicación. Cuando necesito convertir una charla o clase grabada en texto, whisperweb.dev me resulta práctico porque funciona directamente desde el navegador. Gracias de nuevo por compartirlo.
звоните круглосуточно по телефону горячей линии клиники: наши специалисты готовы оказать необходимую помощь в решении проблемы алкогольной зависимости.
Подробнее можно узнать тут – вывод из запоя цена сочи
Вывод из запоя на дому в Казани удобен, когда близкий человек не готов ехать в клинику, плохо переносит дорогу или находится в состоянии сильной слабости. Врач приезжает на дому, сохраняет анонимность, спокойно объясняет процесс и начинает лечение только после осмотра и согласия пациента. Вызов врача на дому особенно важен, если муж, отец, брат, мама или другой близкий уже не может перестать пить и нуждается в срочной помощи.
Исследовать вопрос подробнее – вывод из запоя клиника в казани
Наркологическая помощь клиники направлена не только на снятие острого состояния, но и на дальнейшее лечение алкогольной зависимости. Вывод из запоя на дому подходит пациенту, если нет признаков тяжелого отравления, психоза, судорог и опасных осложнений. Если состояние больного тяжелое, врач может рекомендовать лечение в стационаре клиники, где пациент находится под наблюдением медицинской команды, а терапия проходит безопаснее.
Исследовать вопрос подробнее – анонимный вывод из запоя сочи
Нарколог на дом в Балашихе с выездом врача, оценкой состояния и оказанием необходимой помощи в наркологической клинике «Похмельная служба».
Углубиться в тему – http://narkolog-na-dom-balashiha13-3.ru
основанием для вызова специалиста является неспособность человека самостоятельно выйти из состояния непрерывного употребления алкоголя и наличие признаков абстиненции.
Получить дополнительную информацию – вывод из запоя цена
На странице услуги можно использовать и такую формулировку: нарколог на дом в — экстренная помощь при алкогольной и наркотической зависимости. В Балашихе выездной формат востребован, когда нужна быстрая помощь без поездки в клинику, без ожидания приема и без лишнего внимания соседей.
Узнать больше – http://narkolog-na-dom-balashiha13-2.ru/
Вывод из запоя на дому в Сочи проводится анонимно: соседям, коллегам и третьим лицам не передается информация о состоянии пациента, диагнозе, курсе лечения, факте вызова врача или необходимости дальнейшего наблюдения. Документы оформляются только в пределах медицинской работы, а постановки на учет при обращении в частную клинику не происходит.
Углубиться в тему – наркология вывод из запоя в сочи
Обращаем внимание, что таблица носит ознакомительный характер. Точную программу лечения и финальную цену определяет врач после осмотра и необходимых анализов. Врач нарколог бесплатно ответит на все ваши вопросы по услуге вывода из запоя на дому и оформит вызов врача.
Узнать больше – vyvod-iz-alkogolnogo-zapoya
На первом этапе участник программы сталкивается с признанием бессилия перед зависимостью. Для многих пациентов это трудность, потому что человек может считать, что он способен справиться самостоятельно, что употребление не разрушает его жизнь или что лечение зависимости ему не нужно. В процессе работы он замечает, как болезнь влияет на отношения, работу, здоровье, самооценку, поведение, мысли, эмоции и способность принимать ответственные решения.
Исследовать вопрос подробнее – программа 12 шагов для созависимых
Вывод из запоя в Сочи требуется, когда человек не может самостоятельно выйти из длительного употребления алкоголя, испытывает тяжелое похмелье, тревогу, бессонницу, тошноту, скачки давления, признаки интоксикации или резкое ухудшение состояния. В такой ситуации важно не ждать недели и не подбирать средства самостоятельно: лечение запоя должен проводить врач, потому что при отравлении алкоголем, хронических заболеваниях и приеме большого количества таблеток возможны опасные осложнения.
Подробнее – вывод из запоя на дому недорого сочи
Вывод из запоя в Казани на дому и в клинике: врач-нарколог, капельница, детоксикация, лечение алкоголизма, кодирование, реабилитация — круглосуточная помощь анонимно.
Углубиться в тему – нарколог вывод из запоя казань
выездная наркологическая служба оперативно приедет по указанному адресу, имея при себе все необходимое оборудование и медикаменты, в том числе для оказания неотложной помощи.
Получить дополнительную информацию – наркология вывод из запоя в сочи
Ниже перечислены основные плюсы, которые получает каждый пациент при выборе стационарного лечения алкоголизма в нашей наркологической клинике. Все процедуры проводятся с использованием современного оборудования и сертифицированных лекарств, что абсолютно исключено при попытках лечиться на дому:
Разобраться лучше – вывод из запоя на дому круглосуточно
Сегодня легко вызвать нарколога на дом в Балашиху круглосуточно, просто позвонив по единому телефону нашего специализированного центра в любое время суток, любой день (даже в выходные и праздники). Наркологическая помощь может понадобиться в любое время дня и ночи, поэтому клиника доктора Исаева оказывает широкий спектр услуг, в том числе в домашних условиях, 24/7. Алкогольная зависимость и наркомания — серьёзные заболевания, требующие немедленного квалифицированного вмешательства. Вывод из запоя и лечение алкоголизма на дому или в стационаре начинается с полного осмотра врача-нарколога, диагностики состояния и назначения индивидуальной схемы терапии. Мы гарантируем полную анонимность и конфиденциальность — данные пациента обрабатываются строго в соответствии с политикой обработки персональных данных. Наши специалисты имеют многолетний опыт работы с зависимыми людьми, используют современные и безопасные препараты, позволяющие быстро восстановить организм после отравления алкоголем или наркотиками. Лечение алкоголизма — это процесс, который требует времени и комплексного подхода, но первый шаг к выздоровлению можно сделать уже сегодня. Очень важно не откладывать обращение, ведь каждый день запоя усугубляет состояние здоровья и повышает риск тяжелых осложнений. Вывод из запоя и детоксикация — первый этап на пути к трезвости, и от качества лечения зависит дальнейшая ремиссия.
Углубиться в тему – narkolog-na-dom
Лечение запоя без госпитализации в стационаре Балашихи. Мы предлагаем лечение на дому, без необходимости госпитализации.
Получить больше информации – нарколог вывод из запоя
Вывод из запоя на дому в Сочи подходит пациентам, у которых нет признаков острого психоза, тяжелого отравления, судорог, потери сознания и других состояний, требующих немедленной госпитализации. Врач нарколог приезжает по адресу, проводит обследование, уточняет, сколько дней длится запой, какие препараты человек принимал, есть ли хронические болезни, аллергии, ограничения по здоровью и документы, подтверждающие прошлое лечение.
Детальнее – наркология вывод из запоя в сочи
Ниже перечислены основные плюсы, которые получает каждый пациент при выборе стационарного лечения алкоголизма в нашей наркологической клинике. Все процедуры проводятся с использованием современного оборудования и сертифицированных лекарств, что абсолютно исключено при попытках лечиться на дому:
Подробнее можно узнать тут – вывод из запоя с выездом
Важно не ждать, когда состояние пациента станет критическим. Алкоголизма, наркомании и других форм зависимости часто стесняются, но промедление может привести к осложнениям, депрессии, агрессии, нарушению работы органов, тяжелой интоксикации и риску для жизни человека.
Подробнее тут – нарколог на дом в казани
Наркологическая клиника в Балашихе предлагает срочный вывод из запоя в условиях стационара. Круглосуточная наркологическая помощь позволяет быстро и безопасно вывести человека из тяжелого состояния, вызванного длительным употреблением алкоголя. Лечение алкоголизма в стационаре — это первый и самый важный шаг на пути к полному избавлению от зависимости. Врачи-наркологи нашей клиники проводят комплексную детоксикацию, используют эффективные методы лечения и назначают персональный курс терапии. Каждый пациент получает необходимые медицинские услуги анонимно, с гарантией полной конфиденциальности. Лечение в стационаре обеспечивает круглосуточный контроль за состоянием больного, что особенно важно при серьезных запоях и наличии сопутствующих патологий внутренних органов, сердца и печени. Лечение алкогольной зависимости в стенах специализированной клиники — это возможность получить полноценную помощь и вернуться к трезвой жизни, не откладывая решение проблемы. Очень часто симптомы запоя настолько тяжелы, что справиться с ними собственными силами невозможно, и тогда на помощь приходят опытные доктора нашей наркологической службы.
Исследовать вопрос подробнее – вывод из запоя на дому балашиха цены
Каждый случай вывода из запоя индивидуален. Схема лечения подбирается после диагностики состояния пациента. Врач-нарколог оценивает стаж употребления (иногда он достигает многих лет), стадию алкоголизма, наличие сопутствующих хронических заболеваний и негативных последствий. Лечение в клинике или на дому требует тщательного подхода. Мы используем только проверенные лекарственные препараты и растворы для инфузионной терапии. Капельница при выводе из запоя содержит витамины, ноотропы, глюкозу, гепатопротекторы и седативные компоненты. Такая терапия помогает быстро снять абстинентный синдром, нормализовать работу внутренних органов, вывести токсические вещества и уменьшить слабость. Лечение алкоголизма невозможно без мотивации пациента, поэтому наши психологи и психотерапевты проводят мотивационные беседы, помогая осознать проблему. Лечение — это не только снятие интоксикации, но и изменение отношения к спиртному. Очень важно, чтобы лечение проходило под наблюдением квалифицированных специалистов, имеющих большой опыт в сфере наркологии и психиатрии. Главный врач клиники, Александр Анатольевич, лично контролирует качество оказания услуг, а команда экспертов, включая Дмитрия Николаевича, Ольгу Андреевну и Сергея Сергеевича, ежедневно помогает зависимым людям вернуться к трезвости. Мы используем лучшие методики, чтобы эффективно справляться с самыми сложными случаями алкоголизма и наркомании, и знаем, как облегчить состояние даже в критической ситуации.
Получить дополнительную информацию – вывод из запоя на дому в балашихе
Buen artículo sobre “Historias de Pi: calculando el área del círculo”; se nota el cuidado en la explicación. Cuando necesito convertir una charla o clase grabada en texto, whisperweb.dev me resulta práctico porque funciona directamente desde el navegador. Gracias de nuevo por compartirlo.