Cuadrados latinos

Hace unos días hablábamos de cuadrados mágicos y prometimos hablar también de cuadrados latinos; hoy será el día. Digamos antes de nada, que un cuadrado latino es una matriz de n×n elementos en la que cada casilla está ocupada por uno de los n símbolos, de tal modo que cada uno de ellos aparece exactamente una vez en cada columna y en cada fila.

Lo primero que debemos tener en cuenta es que un cuadrado latino no se forma sólo con números, sino que vale cualquier tipo de símbolos. Vemos por ejemplo en la fotografía encima de estas líneas, este cuadrado latino formado por cuadraditos de diferentes colores, y que compone un vitral en el salón comedor del Gonville y Caius College, en Cambridge, Inglaterra. Este vitral honra la memoria del estadístico y biológo Sir Ronald Aylmer Fisher, quien lo usó en sus experimentos.

Los cuadrados latinos son conocidos desde la antigüedad, y ya los árabes e indios los usaban como amuletos. Una aparición más moderna ocurre en el siglo XIII, cuando el filósofo Ramón  Llull  (1232-1315)  introduce en  su  texto  Ars  Demostrativa  (1283)  cuatro cuadrados latinos de orden 4, utilizando como símbolos los cuatro elementos: fuego, aire, agua y tierra.

Una definición formal es debida a Leonhard Euler, quien en 1799 estaba interesado en dar solución al llamado Problema de los 36 oficiales. Dicho problema consiste  en ver si es posible colocar en un cuadrado de tamaño  6×6, a treinta y seis oficiales de seis regimientos diferentes y que de cada regimiento haya uno de los seis distintos grados, de forma que no coincidan dos oficiales  del  mismo rango o del mismo regimiento en ninguna fila y en ninguna columna.

De hecho, en su artículo Recherches sur une nouvelle espece de quarres magiques, publicado en la revista Verhandelingen uitgegeven door het zeeuwsch Genootschap der Wetenschappen te Vlissingen en 1782, Leonard Euler escribe:

Una cuestión muy curiosa que ha desafiado la inteligencia de muchas personas, me inspiró para emprender la siguiente investigación que al parecer ha abierto una nueva trayectoria dentro del Análisis y, en particular, en Combinatoria. Esta cuestión concierne a un grupo de treinta y seis oficiales de seis rangos diferentes, tomados de seis regimientos distintos, y distribuidos en un cuadrado de tal forma que en cada fila y cada columna haya seis oficiales, cada uno de diferente rango y regimiento. Pero, después de dedicar muchos esfuerzos a resolver este problema, tenemos que reconocer que tal disposición es absolutamente imposible, aunque no podemos ofrecer una prueba rigurosa.

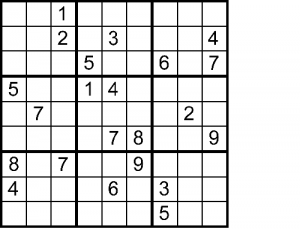
Generar cuadrados latinos ha sido siempre un pasatiempo de muchos aficionados a las matemáticas, y una de sus versiones modernas son precisamente los sudokus, en los que la restricción adicional es que cada uno de los subgrupos de 3×3 que lo forman debe debe contener todos los dígitos del 1 al 9.

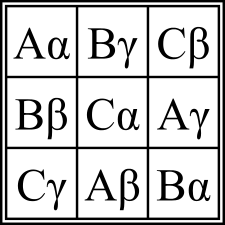
Hay tipos especiales de cuadrados latinos, como los cuadrados greco-latinos, cuadrados de Euler o cuadrados latinos ortogonales de orden n. Éstos, son cuadrículas cuadradas n×n de elementos de dos conjuntos S y T, ambos con n elementos, cada celda conteniendo un par ordenado (s, t).  Aquí, s es un elemento de S y t es un elemento de T, de forma que cada elemento de S y cada elemento de T aparezca exactamente una vez en cada fila y en cada columna y que no haya dos celdas conteniendo el mismo par ordenado. Este es uno de los ejemplos que manejaba Euler, quién probó muchos resultados:

Obviamente, un cuadrado greco-latino puede descomponerse en dos ortogonales.

El estadístico inglés Ronald Fisher, de quién hemos hablado al principio,  usó los cuadrados latinos para mejorar los métodos agrícolas, cuando se hallaba investigando la eficacia de los fertilizantes en el rendimiento de las cosechas. Buscó la manera de plantar cosechas en similares condiciones de suelo, de modo que la calidad de la tierra no fuese un factor indeseable que influyese en el rendimiento de la cosecha. Si bien la única manera de asegurarse de tener condiciones idénticas de tierra era utilizar siempre el mismo suelo, en la práctica esto es casi imposible, pues se deberían desenterrar y volver a plantar las cosechas varias veces.

Si se tuviese un campo cuadrado dividido en 16 parcelas, puede construirse un cuadrado latino en que la descripción del campo sea tal que la calidad del suelo varíe «vertical» y «horizontalmente». Entonces, se aplican al azar los 4 fertilizantes («a», «b», «c», y «d») con la única condición de que cada fertilizante aparezca una sóla vez en cada fila y en cada columna. De esta manera se busca eliminar la variación de la calidad de tierra. Si hubiese otro factor que pudiese influir en el rendimiento, por ejemplo, el momento del día (A, B, C, D) en que se aplica el tratamiento, entonces puede utilizarse un cuadrado latino ortogonal al anterior, donde se identifiquen dichos momentos del día. DAsí, cada pareja momento-fertilizante se aplicará en una única parcela.

Terminamos con una fotografía del cuadrado latino más famoso que se ha utilizado en diseño de experimentos. Fue elaborado por Fisher en 1926, y llevado a la práctica en 1929 en el Bosque Beddgelert, en el norte de Gales, para estudiar el  comportamiento de cinco tipos de árboles.

______

Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, ICSU) y Cristina Sardón (ICMAT-CSIC).

Guardar

Guardar

Guardar

Guardar

Guardar

Guardar

Guardar