![]()
Maryna Viazovska, segunda medallista Fields de la historia
El pasado 5 de julio se anunciaron en Helsinki los ganadores de las medallas Fields correspondientes al International Congress of Mathematicians 2022. Una de las grandes esperanzas es que alguno de los posibles cuatro premiados fuera una mujer y estas se cumplieron en la persona de Maryna Viazovska.

Viazovska ya era profesora en Lausana cuando el presidente de la Unión Matemática Internacional (IMU) le anunció en febrero que se le había concedido la medalla Fields. Recordemos que estos premios no se hacen públicos hasta el día de la inauguración del correspondiente ICM. Sin embargo, su familia todavía permanecía en Kiev. Sus dos hermanas, una sobrina de 9 años y un sobrino de 8 partieron hacia Suiza; tras los avatares propios de los refugiados, el 4 de marzo llegaron a Lausana, donde se alojaron con Viazovska, su marido, su hijo de 13 años y su hija de 2 años. Sus padres y el resto de su familia permanecen en Ucrania, sujetos a la locura desatada por Vladimir Putin.
Maryna Viazovska realizó sus estudios de licenciatura en la Universidad Nacional Taras Shevchenko de Kiev, su máster en la Universidad Técnica de Kaiserslautern, doctorándose en 2013 en Bonn. Fue investigadora postdoctoral en el Instituto de Altos Estudios Científicos y en la Universidad Humboldt de Berlín, y en 2017 fue Minerva Distinguished Visitor en la Universidad de Princeton. Se incorporó a la EPFL en 2017 como profesora titular y fue promovida a catedrática en 2018.
Maryna fue una niña con una gran capacidad para las matemáticas, aunque no triunfó cmo ella pensaba en las Olimpiadas Matemáticas. En sus entrevistas en Helsinki, recordaba a la matemática Yulia Zdanovskaya, ganadora de una medalla de plata en la Olimpiada Matemática Femenina Europea, y profesora en Secundaria, asesinada este año por las tropas rusas a la edad de 21 años, una noticia que conmocionó al mundo matemático.
Su primer gran resultado es darle un nuevo enfoque al llamado problema de los diseños esféricos. Un diseño esférico es un conjunto finito de puntos en la esfera unidad Sd tal que el valor medio de cualquier polinomio f de grado t o menos en el conjunto es igual al valor medio de f en toda la esfera (es decir, la integral de f sobre Sd dividida por el área de Sd). El concepto de diseño esférico se debe a Delsarte, Goethals y Seidel (Delsarte, P.; Goethals, J. M.; Seidel, J. J. (1977), Spherical codes and designs, Geometriae Dedicata, 6 (3): 363–388.)
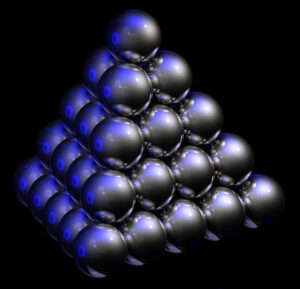
Tras este logro, Viazovska abordó un imporatnte problema matemático, el empaquetamiento de esferas de manera que los spacios que se dejan entre ellas sea el mínimo posible. El problema viene de la llamada conjetura de Kepler, quien había compartido correspondencia con el astrónomo y matemático inglés Thomas Harriot, acerca de la manera óptima de apilar balas de cañón en la cubierta de un buque. Sir Walter Raleigh, de quién Harriot fue ayudante, le había planteado la cuestión cuando estaban planificando una expedición en 1585 rumbo a Virginia, a fin de establecer allí la primera colonia británica. Además, Kepler escribe su ensayo “Strena seu de nive sexángula”, donde afirma que la forma particular de los copos de nieve debe ser consecuencia de la manera en la que se empaquetan las partículas que los constituyen.
Auqnue en algunos titulares de periódicos hemos leído que la medalla Fields se le concede a Viazovska por descubrir como empaquetar naranjas en 24 dimensiones (nos gustaría por cierto que los priodistas científicos dejaran de lado esas analogías que llevan a la gente a pensar qué para que se nos da dinero de sus impuestos), la realidad es que los resultados logrados por Viazovska son fundamentales por sus aplicaciones a los códigos de corrección de errores.
El problema del empaquetamiento de esferas, resuelto en dimensiones 2 y 3, no era así en dimensiones superiores. El uso de formas modulares permitía decir algo en dimensión 8, hasta que Viazovska inventó lo que se llama un forma cuasimodular desconocida que daba el resultado, tal y como describió en su artículo The sphere packing problem in dimension 8, Ann. Of Math. (2)185(2017), no. 3, 991–1015. Era una epecie de “función mágica” que probaba que el empaquetamiento óptimo er el llamado retíulo E8.
Con la ayuda de sus colaboradores habituales (Andriy Bondarenko y Danylo Radchenko) a los que se añadió Henry Cohn, lo intentan en dimensión 24, y demuestran que la máxima densidad de empaquetamiento de esferas en esa dimensión se consigue con el empaquetamiento de retícula de Leech y, salvo escalamientos e isometrías, en, es el único empaquetamiento periódico de esta densidad. El esultado se publica en el artículo The sphere packing problem in dimension 24. Ann. of Math. (2)185(2017),no. 3,1017–103.
En el extraordinario artículo que Quanta magazine le ha dedicado, Maryna termina con una frase que debería ser de lectura obligatoria para autócratas: “los tiranos no pueden impedir que hagamos matemáticas. Al menos hay algo que no nos pueden quitar». Tampoco la esperanza.
______________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).