![]()
Ver para pensar
«En muchos casos, una demostración farragosa puede ser sustituida por una geométrica análoga, tan simple y bella que la veracidad de un teorema es casi vista en una ojeada», Martin Gardner, 1973
Los Libros de la Catarata, la Federación Española de Profesores de Matemáticas y el Instituto de Ciencias Matemáticas del CSIC continúna su colaboración editorial con un nuevo título de la colección Miradas Matemáticas, y esta vez es el turno de Demostraciones visuales en matemáticas. Ver para pensar, de Ana Carvajal Sánchez y José Luis Muñoz Casado.
Ya hemos reseñado en Matemáticas y sus fronteras los volúmenes que han ido apareciendo desde la puesta en marcha de Miradas Matemáticas, una colección que trata de combinar divulgación y didáctica con el fin de acercar la disciplina tanto a los profesores como a cualquier persona que guste de la ciencia.
En este libro se aborda uno de los temas más populares de las matemáticas, las llamadas demostraciones visuales. Recordemos el dicho de “una imagen vale más que mil palabras”, aunque en este caso, la palabra demostrcaión debe entenderse de una manera más informal: las imágenes ayudan pero no pueden sustituir a la prueba formal sin la que las matemáticas perderían su esencia (Euclides ya nos lo adelantó, veáse la entrada Dibujos que ayudan a probar teoremas).
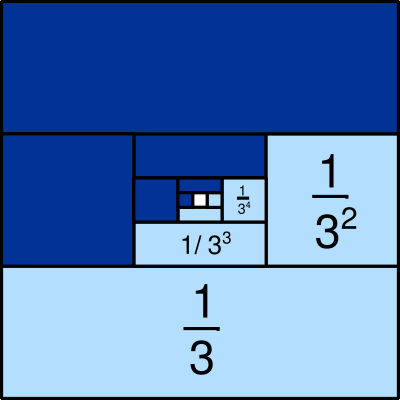
Como se dice en la descripción del libro, “las imágenes siempre han sido un poderoso recurso para, entre otras funciones, transmitir información o representar la realidad. En las matemáticas, la realización de esquemas, diagramas, dibujos, etc., sirve para mostrar o ejemplificar complejas ideas matemáticas de forma sencilla. Este libro es una introducción a las llamadas demostraciones visuales en matemáticas. Aunque no son estrictamente demostraciones formales, se trata de imágenes que permiten visualizar con claridad ciertas propiedades o teoremas, comprender y resolver mejor los razonamientos y problemas matemáticos y estimular la generación de ideas.”
Hablamos pues de demostraciones sin palabras, que la imagen lo diga todo. En el libro se traza un recorrido histórico de las demostraciones visuales, que se remontan a la antigua China, la Grecia clásica o la India del siglo XII.
El Teorema de Pitágoras ha sido siempre un referente en este tema, ya lo citamos en una anterior entrada, Perigal, el británico que incluyó su demostración del Teorema de Pitágoras en sus tarjetas de visita, pero añadimos ahora este video que nos muestra en un minuto seis demostraciones visuales del teorema
[youtube]https://www.youtube.com/watch?v=-HA1w_IOpnQ[/youtube]
Sobre los autores
Ana Carvajal Sánchez es matemática, especialista en metodología y didáctica de las Matemáticas en las etapas de Educación Infantil, Primaria y Secundaria. Es autora y editora, y compagina su oficio con su actividad de formación a estudiantes y docentes.

José Luis Muñoz Casado es matemático y posee el título de máster en Investigación matemática. Ha escrito varios libros y artículos en diversas revistas de educación matemática. Coordina la sección «CreoGebra» de la revista SUMA y es el actual presidente de la Sociedad Madrileña de Profesores de Matemática.

___
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias).


I was very satisfied to find this site. I required thanking you for this great read!! I absolutely enjoyed every little bit of it and I have you bookmarked to check out novel matter you post. I am really first time here. I approach across this blog and I find it truly useful & it helped me out much. I hope to offer amazing back and help others like you helped me
La geometría, es una forma de filosofar sobre las formas de las cosas de la realidad, herramienta intelectual abstracta, que el Demiurgo, Dios Creador, inspirado por Platón, utilizó para diseñar todo lo que existe, desde su taller artesanal. Y en la ascensión hacia el episteme o idea Del Bien, posee la tercera posición por arriba de la Techne. Desde el primer filósofo, Tales de Mileto presocrático, planteo teoremas geométricos esclarecedores, llevándolos a la práctica, al intentar medir la altura del pirámides de Egipto. Si es que la práctica geométrica es una especie de calistenia abstracta filosófica, que nos permite acceder al alma que da vida, función y forma, a las casos de la realidad circundante, sean naturales o artificiales, ya que todo lo que existe atiende a una determinada geometría.