![]()
La máquina de Galton
Siempre que puedas, cuenta
Sir Francis Galton
No es la primera vez que Francis Galton se asoma a Matemáticas y sus fronteras. En El matemático que quiso medir la inteligencia hablamos de sus estudios sociológicos y antropológicos , y en La extinción de los apellidos entre la aristocracia victoriana y el número R sobre el ahora famoso número R en el caso de la transmisión vertical. Pero hoy nos centraremos en uno de sus diseños, la llamada máquina de Galton.
Galton nació en Birmingham, el 16 de febrero de 1822, y falleció en Haslemere, Surrey, el 17 de enero de 1911). Se le puede calificar de polímata, porque sus intereses y actividades fueron de lo más variado y abarcaban la estadística, la sociología, la psicología, antropología, geografía, y muchas más cosas.
Galton fue pionero en la aplicación de los métodos estadísticos a las ciencias sociales y a la medicina, también a la meteorología. En realidad, fue por esas aplicaciones por lo que Galton se dedicó a estudiar la estadística. En las citadas entradas previas podemos encontrar muchos más detalles.
En Estadística nos interesa conocer los valores medios y como las mediciones se dispersan en torno a estos. A finales de 1860, Galton fue capaz de proponer la llamada desviación estándar. En su estudio de la distribución normal, Galton inventó una máquina que se llamó la Máquina (o Tablero) de Galton. Su objetivo era demostrar el teorema del límite central, en particular que, con una muestra lo suficientemente grande, la distribución binomial se aproxima a la distribución normal. Como comentamos, su curiosidad era conocer por qué ciertas características humanas, como la altura, en lugar de variar aleatoriamente dentro de una población, parecían variar dentro de una cierta estructura, una distribución normal. Galton quería precisamente era proporcionar una demostración práctica de por qué ocurre este hecho (aparte, por supuesto, de la demostración matemática, basada en el Teorema Central del Límite).
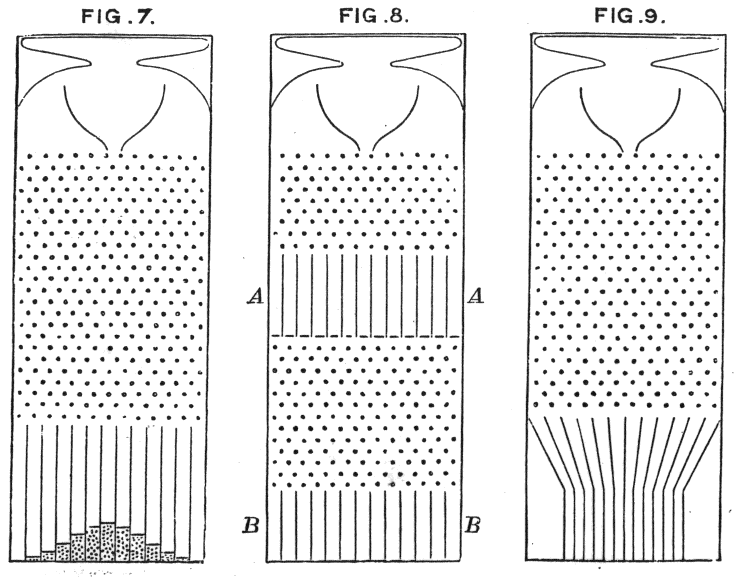
El Tablero de Galton consiste en un tablero vertical en el que se van intercalando filas de clavijas tal y como se muestra en la imagen. Ahora vamos dejando caer desde arriba cuentas o bolitas que van rebotando en las clavijas. Al golpearlas, pueden rebotar a la izquierda o hacia la derecha. Las cuentas acaban agrupándose en los recipientes de la base del tablero, y uno observa como las alturas de las columnas se aproxima a la curva de campana. La razón de esto es que hay muchas más formas de llegar a estos contenedores centrales que a los extremos. En efecto, aunque la probabilidad de ir a un lado o a otro es de ½, hay más maneras de irse hacia el centro que hacia los lados.
La fascinanción de Galton por la curva de campana queda de manifiesto en su libro Herencia Natural, publicado en 1889:
Orden en el Caos Aparente: Sé de casi nada tan apto para impresionar la imaginación como la maravillosa forma de orden cósmico expresada por la Ley de la Frecuencia del Error. La ley habría sido personificada por los griegos y deificada, si hubieran sabido de ella. Reina con serenidad y en completo olvido en medio de la más salvaje confusión. Cuanto más grande es la multitud, y cuanto más grande es la anarquía aparente, más perfecto es su dominio. Es la ley suprema de la irracionalidad. Cada vez que una gran muestra de elementos caóticos son tomados en mano y reunidos en el orden de su magnitud, una insospechada y más bella forma de regularidad demuestra haber estado latente todo el tiempo.
___________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).


El Tablero de Galton consiste en un tablero vertical en el que se van intercalando filas de clavijas tal y como se muestra en la imagen. Ahora vamos dejando caer desde arriba cuentas o bolitas que van rebotando en las clavijas. Al golpearlas, pueden rebotar a la izquierda o hacia la derecha. Las cuentas acaban agrupándose en los recipientes de la base del tablero, y uno observa como las alturas de las columnas se aproxima a la curva de campana. La razón de esto es que hay muchas más formas de llegar a estos contenedores centrales que a los extremos. En efecto, aunque la probabilidad de ir a un lado o a otro es de ½, hay más maneras de irse hacia el centro que hacia los lados.
otima materia gostei
me ajudou em um trabalho academico
Thanks a lot for your sharing
Brigade Valencia Apartments Bangalore.
no hate saludos
Qué interesante volver a Francis Galton en ‘Matemáticas y sus fronteras’. Me encanta cómo este post subraya su naturaleza polímata y sus diversas contribuciones, desde la estadística a la antropología. ¡Tengo ganas de leer sobre su famosa máquina de Galton, que siempre me ha intrigado!
escape road city 2: El Tablero de Galton es un dispositivo vertical con clavijas donde bolitas rebotan al caer, agrupándose en recipientes en la base. Esto forma una distribución en forma de campana, ya que hay más formas de llegar al centro que a los extremos, a pesar de que la probabilidad de desviarse es de ½.
Este artículo ofrece una mirada fascinante a la máquina de Galton y su importancia en la estadística. Para los amantes de la lógica, también pueden visitar el juego Enhanced Queens Game para más desafíos estratégicos.
Muy buen artículo sobre esos conceptos matemáticos — realmente ayuda a visualizar ideas complejas de forma clara. Si alguna vez te interesa aprender más sobre trámites digitales en India (por ejemplo licencias, registro de vehículos), checa Parivahan Sewa para verlo en práctica.
Pelota Libre TV: Ver Futbol Libre online en vivo y directo. Disfruta de partidos de la Copa Libertadores, Sudamericana y del fútbol argentino como River Plate y Boca Juniors. Canales como TyC Sports, ESPN, Fox Sports y TNT transmiten eventos internacionales gratis.
Me encanta cómo este artículo vuelve a traer a Galton al blog, un personaje tan fascinante. Es genial ver cómo sus múltiples facetas, desde la estadística hasta la antropología, son destacadas. ¡Ya tengo ganas de aprender sobre la máquina de Galton, que es el foco de esta entrada!
Me fascina la versatilidad de Francis Galton como polímata. Su máquina de Galton es un diseño ingenioso que refleja su genio multidisciplinario. ¿Cómo crees que sus diversas áreas de inter
Futbol libre destaca por ofrecer transmisiones de fútbol en línea con acceso sencillo y sin procesos complicados. Es una plataforma buscada por fanáticos que quieren mantenerse informados y ver partidos importantes en tiempo real.