![]()
Historias de pi: Cuando Sir Francis Galton nos enseñó como dividir una tarta redonda
El 20 de diciembre de 1906, sir Francis Galton publicó un breve artículo en la sección de Cartas al Editor de Nature con el título: «Cutting a Round Cake on Scientific Principles» (“Dividiendo una tarta redonda siguiendo principios científicos”). La comentamos en esta entrada porque es una auténtica curiosidad de un científico tan relevante como Galton.

Galton escribe:
NAVIDAD sugiere tartas, y estas el deseo por mi parte de describir un método de cortarlas que he ideado recientemente para mi propia diversión y satisfacción. El problema a resolver era: “dado una tarta de te redonda de unas 5 pulgadas de ancho, y dos personas de moderado apetito para comerla, de qué manera debería dividirse para dejar un mínimo de superficie expuesta a secarse”. El método ordinario de cortar una cuña es muy defectuoso en este sentido. El resultado que hay que conseguir es cortar el pastel de forma que las porciones restantes encajen.
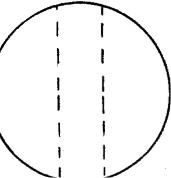
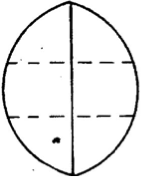
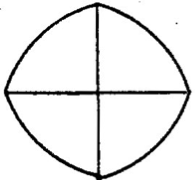
El texto incluye unas figuras
con este texto explicativo debajo:
Las líneas a trazos muestran el corte previsto. Las líneas rectas continuas muestran los cortes realizados. Los trozos se mantienen juntos mediante una banda elástica común que encierra el conjunto. En las figuras anteriores, cada una de las dos operaciones sucesivas elimina aproximadamente un tercio de la superficie del disco original.
En consecuencia, las cuerdas (o los arcos) de las circunferencias de estas porciones deben ser iguales. La dirección de los dos primeros planos verticales de la sección no es importante; pueden pueden ser paralelos, como en la primera figura, o pueden encerrar una cuña. Los cortes que se muestran en las figuras representan aquellos de dejar que la tarta dure tres días, cada operación sucesiva ha eliminado aproximadamente un tercio de la superficie del disco original. Una banda de goma común abraza el conjunto y mantiene los trozo unidos.
F.G.
Repartir tartas entre varios comensales es un problema matemático que da mucho juego, sobre todo si se quiere hacerlo de manera equitativa. Por ejemplo, en este video
[youtube]https://www.youtube.com/watch?v=kaMKInkV7Vs&feature=emb_logo[/youtube]
se indica una manera de hacer el reparto cuando tenemos tres participantes, método generalizable a muchos más, lo que complicaría muchísimo el proceso. En el video no se trata en realidad de un problema de geometría, más bien de teoría de la elección.
Como hablamos de tartas redondas, la geometría si nos da pistas. Lo habitual es dividir la tarta en cuñas (sectores circulares) iguales, porque nos vamos a comer toda la tarta ya, y no tenemos la preocupación de Sir Francis Galton de que se reseque. Y para hacerlo, ya sabemos que los sectores circulares deben ser iguales, y si está presente un matemático, le pueden pedir que divida 360º entre el número de comensales (la broma usual). Y ya puestos, que calcule el área y el volumen de cada trozo resultante (pi en danza).
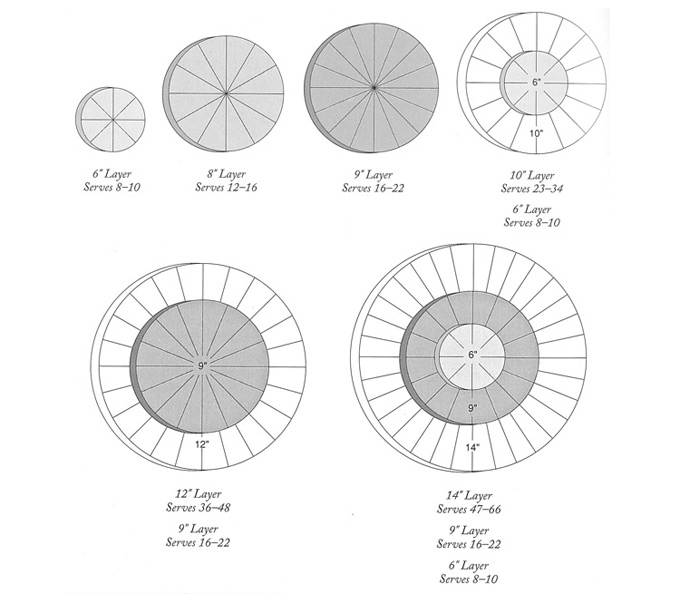
Pero si la tarta es muy grande, las cuñas pueden ser demasiado largas y poco manejables. En este artículo, Cómo cortar un pastel redondo grande para que salgan porciones decentes, hemos encontrado una solución muy ingeniosa. Se trazan dos circunferencias, tal y como se ve en la figura, y se cortan las cuñas, pero ahora ya son más cortas, tal y como en el video. Con el centro, vale la sugerencia del video o dividirlo a su vez
[youtube]https://www.youtube.com/watch?v=u3umyGQ-E5I&feature=emb_logo[/youtube]
Solo me queda pedirles que disfruten de la tarta.
___________
Manuel de León (CSIC, Fundador del ICMAT, Real Academia de Ciencias, Real Academia Canaria de Ciencias, Real Academia Galega de Ciencias).

The best free sexy chat contacts with a hot ladies only at hausfrauen sexkontakt! Check out right now and you will not regret it at all!